URL: https://belle2.desy.de/e101530/e111982/@@siteview
Breadcrumb Navigation
Software Development
Calorimeter reconstruction
(Young Investigators Group of Torben Ferber)
We work on the reconstruction of photons in the electromagnetic calorimeter (ECL) of Belle II. We are leading the ECL reconstruction software development with a strong focus on Machine Learning including Deep Neural Networks to improve photon detection and reconstruction.
Track-based alignment and calibration
The study of CP violating effects requires very accurate reconstruction of decay vertices of the B-mesons and their anti-particles with the help of the vertex detector. Therefore it is of utmost importance to align and calibrate these detectors as precisely as possible. Building on its extensive experience with alignment and calibration of tracking detectors in H1 and CMS based on the MillePede algorithm and the General Broken Line (GBL) concept as track model the DESY group is working on alignment and calibration procedures for the Belle II tracking system.
The aim of track-based alignment and calibration is the determination of all parameters effecting the position measurement in the tracking detectors from the track data itself. For single measurements or single tracks parameters can be highly correlated. From a diversity of track samples with different track topologies and operational conditions all the parameters can be estimated accounting for remaining correlations. The Millepede algorithm implements a linearization of this problem.
Millepede-II
Millepede uses a linearization of the track model (f) to calculate corrections to initial values of the ''global'' (alignment and calibration) parameters (p). The minimization of the sum (over all tracks and hits) of the scaled residuals from the (scalar) measurements (m) (see equation below) with respect to all global and ''local'' (track) parameters (q) leads to a huge linear equation system. With block matrix algebra this can be reduced to a system of the size of the number of global parameters. This allows to obtain all global parameters keeping the correlations due to all the tracks. It requires the complete covariance matrix from all local (track) fits. The local fit is implemented as a simultaneous determination of all track parameters from all hits (linear least squares) in contrast to progressive procedures like a Kalman filter. In cases where the multiple scattering in the detector material makes a significant contribution to the resolution a track fit based on General Broken Lines can be used. This is mathematically equivalent to a Kalman filter, but computationally different.
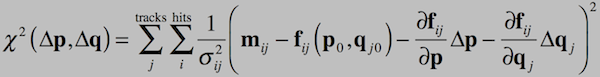
The solution (x) of the large linear equation system (A*x=b) is obtained by inversion, diagonalization or the MINRES method (iteratively minimizing |A*x-b|). For outlier down-weighting or rejection internal iterations are performed.

Millepede-II is supported by the statistics tools group of the analysis center of the Helmholtz Terascale alliance. WIKI
General Broken Lines
For a track with an initial trajectory from a prefit of the measurements (internal seed) or an external prediction (external seed) the description of multiple scattering is added by offsets in a local system. Along the initial trajectory points are defined which can describe a measurement or a (thin) scatterer or both. Measurements are arbitrary functions of the local track parameters at a point (e.g. 2D: position, 4D: slope+position). The refit provides corrections to the local track parameters (in the local system) and the corresponding covariance matrix at any of those points. Outliers can be down-weighted by use of M-estimators.
The broken lines trajectory is defined by (2D) offsets (u) at the first and last point and all points with a scatterer. The prediction for a measurement is obtained by interpolation of the enclosing offsets and for triplets of adjacent offsets kink angles are determined. This requires for all points the jacobians for propagation to the previous and next offset. These are calculated from the point-to-point jacobians along the initial trajectory.
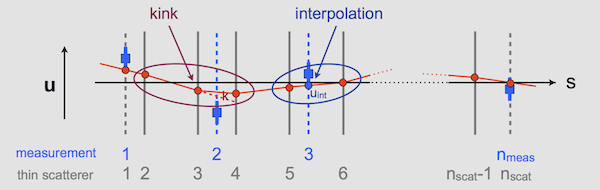
(Simple trajectory in one plane, no curvature, measurements perpendicular to track direction, homogeneous material)
The parameters of this linear least squares fit are a common curvature correction and the local offsets u. The matrix of the corresponding linear equation system has a bordered (from curvature) band (from offsets) structure. For the offset part a fast solution is possible by root-free Cholesky decomposition and forward/backward substitution. The effort to calculate the complete solution (covariance matrix) is linear (quadratic) in the number of scatterers respectively measurements. (With simple inversion this dependencies would be cubic.)
Additional local or global parameters can be added and the trajectories can be written to special binary files for calibration and alignment with Millepede-II.

General Broken Lines are supported by the statistics tools group of the analysis center of the Helmholtz Terascale alliance. WIKI
Parameters
Silicon strip and pixel detectors (like CMS )
Typically the alignment needs to determine for each silicon module the position, orientation and (surface) deformation and the calibration the drift direction (Lorentz angle).
Drift chambers (like H1)
Typically the alignment needs to determine for each anode wire the position, orientation and (gravitational or electrostatic) deformation and the calibration for the space-time-relation. This includes global and local drift velocity and direction and (drift) time offset and their dependencies on variations of the electric and magnetic fields.
Data samples
Beam related particles
A primary data sample are the physics events from the beam-beam-interactions. As (almost) all tracks are coming from the (very) small interaction region the longitudinal and transverse directions are correlated. To overcome this limitation data from various positions of the interaction region along the beam line ("shifted vertex") or beam-gas or beam-wall interactions (inside the detector) are helpful.
Muons from cosmic radiation
The cosmics are a very important data sample. They are uncorrelated to the interaction position and timing, connect two detector halves and in contrast to beam-related data could be taken with various operational conditions like zero magnetic field. One drawback is the azimuthal asymmetry. To catch the rare horizontal events the trigger should apply in addition to the typical up-down coincidence a left-right coincidence too.
Combined objects
In addition to single tracks objects constructed from several tracks could be used. An example is the decay of (narrow) resonances in two charged particles. The mass reconstructed from the decay tracks could be used as additional (virtual) measurement supplying an absolute momentum scale.
External measurements
External measurements (of arbitrary linear combinations of global parameters) can be used in addition to track data by Millepede-II.
Validation
The resulting alignment and calibration has to be verified for the performance (improvement) for physics analysis.
With correct input (proper modeling of detector by track reconstruction) for a linear problem the linear least squares solution is optimal. For non-linearities the linearization point can be improved by iterating the alignment and calibration procedure. Shortcomings of the detector modeling can lead to inconsistencies especially if they effect data samples differently.
References
Alignment and calibration
- H1 alignment experience , C. Kleinwort, Proceedings of the LHC Detector Alignment Workshop, September 4 - 6 2006, CERN, pp. 41-49
- Alignment of the CMS silicon tracker – and how to improve detectors in the future, C. Kleinwort, F. Meier, NIM A, 650 (2011) pp. 240–244, doi:10.1016/j.nima.2010.11.187
- Fast alignment of a complex tracking detector using advanced track models, V. Blobel, C. Kleinwort, F. Meier, Computer Phys. Communications (2011), doi:10.1016/j.cpc.2011.03.017
- Alignment of the CMS Silicon tracker, G. Flucke (on behalf of the CMS collaboration), Proceedings of ACAT2011, Journal of Physics: Conference Series, Volume 368 (2012), doi:10.1088/1742-6596/368/1/012036
Millepede-II
- A New Method for the High-Precision Alignment of Track Detectors, Volker Blobel and Claus Kleinwort, Proceedings of the Conference on Adcanced Statistical Techniques in Particle Physics, Durham, 18 - 22 March 2002, Report DESY 02-077 (June 2002) and hep-ex/0208021
- Software alignment for Tracking Detectors, V. Blobel, NIM A, 566 (2006), pp. 5-13, doi:10.1016/j.nima.2006.05.157
- Draft Millepede-II manual, V. Blobel (2007)
GBL
- A new fast track-fit algorithm based on broken lines, V. Blobel, NIM A, 566 (2006), pp. 14-17, doi:10.1016/j.nima.2006.05.156
- General Broken Lines as advanced track fitting method, C. Kleinwort, NIM A, 673 (2012), pp. 107-110, doi:10.1016/j.nima.2012.01.024


